purescript-uncurried-transformers

Stack-safe monad transformers implemented using continuation-passing style and uncurried functions.

spago install uncurried-transformers

At the surface-level, the only significant difference between this library and transformers is that runner functions like runStateT, runReaderT accept the monadic actions as their last arguments. Unlike in Haskell where the record accessor dictates that it should be first, we have no such restriction in PureScript, hence, the decision to use more convenient and composable syntax.

uncurried-transformers, as the name and description implies, is implemented using uncurried functions and continuation-passing style. The core type, RWSET, is implemented as a newtype over Fn6 with a bunch of seemingly magical parameters:

newtype RWSET r w s e m a = RWSET
  ( forall c
     . Fn6
         -- Environment
         r
         -- State
         s
         -- Trampoline
         ((Unit -> c) -> c)
         -- Lift
         (m (Unit -> c) -> c)
         -- Error
         (Fn3 s e w c)
         -- Success
         (Fn3 s a w c)
         -- Continuation
         c
  )

In essence, this is a JavaScript function with 6 (uncurried) arguments, the first two being the Reader environment and the State state, and the following four being special callbacks which help produce some opaque c type, which is also used as the return type for our uncurried function. What c represents doesn't matter right now, but it's important to look out how these callbacks may be used. Let's take a look at some instances for RWSET:

The Applicative instance, for example, runs the success continuation done in order to produce a c to be returned; it's passed the current state, a result a for the monadic action, and a mempty result for the writer.

instance Monoid w => Applicative (RWSET r w s e m) where
  pure a = RWSET
    ( mkFn6 \_ state _ _ _ done ->
        runFn3 done state a mempty
    )

On the other hand, the MonadThrow instance runs the failure continuation error, in order to produce a c to be returned; it's passed the current state, an error e for the monadic action, and a mempty result for the writer.

instance Monoid w => MonadThrow e (RWSET r w s e m) where
  throwError e = RWSET
    ( mkFn6 \_ state _ _ error _ ->
        runFn3 error state e mempty
    )

The Functor instance demonstrates a basic use of the trampoline continuation more; what it essentially does is that it "thunks" a result c such that some stack space is freed before it's evaluated, effectively making it lazy. In order to map an f over RWSET, we have to run k with a custom done callback such that f is applied over the result a. As a rule of thumb, we use more liberally in order to preserve the stack-safety of our program.

instance Functor (RWSET r w s e m) where
  map f (RWSET k) = RWSET
    ( mkFn6 \environment state0 more lift' error done ->
        more \_ -> runFn6 k environment state0 more lift' error
          ( mkFn3 \state1 a w ->
              more \_ -> runFn3 done state1 (f a) w
          )
    )

Last but not least, the lift continuation acts as a thunk over the base monad m, much like more acts as a thunk for non-monadic values. For MonadTrans, we effectively take the m a and turn it into m (Unit -> c), before being passed to lift for the final c value.

instance Monoid w => MonadTrans (RWSET r w s e) where
  lift m = RWSET
    ( mkFn6 \_ state _ lift' _ done ->
        lift' (map (\a _ -> runFn3 done state a mempty) m)
    )

Hold on, if the c type is completely opaque, then how are we supposed to run the RWSET monad? The answer lies in the fact that we can reify c into "any" type that we want, but for this library in particular, we choose to reify the continuations in the form of an ADT. Notice how each variant of the following type corresponds to the continuations in RWSET, except each c is replaced with a concrete type. Similarly, we can just encode the failure and success continuations using an Either!

data RunRWSET r w s e m a
  = More (Unit -> RunRWSET r w s e m a)
  | Lift (m (Unit -> RunRWSET r w s e m a))
  | Stop s (Either e a) w

Using an ADT allows us to write a tail-recursive loop that "interprets" the RWSET monad, as shown in the code block below. Focusing first on the latter half, we can see that the uncurried function k is ran with the environment r, the state s, the More constructor as the trampoline, the Lift constructor as the lift, and Stop to encode Either an error e or a result a, along with the final state s and the writer result w.

runRWSET r s (RWSET k) =
  let
    go step = case step unit of
      More n ->
        go n
      Lift m ->
        Loop <$> m
      Stop s' a w ->
        pure $ Done $ s' /\ a /\ w
  in
    tailRecM go \_ ->
      runFn6 k r s More Lift
        (mkFn3 \s' e w -> Stop s' (Left e) w)
        (mkFn3 \s' a w -> Stop s' (Right a) w)

We then analyze its result using the auxiliary function go. If the result of running k is More, we tail-recurse into go with the thunk n; if the result is Lift, we tail-recurse into go (with the help of tailRecM) such that the monadic action is ran before the thunk is evaluated; if the result is Stop, we just signal to tailRecM that we're done computing and we have our final result. This tail-recursive loop is what allows us to keep stack-safety at the cost of some heap allocations.

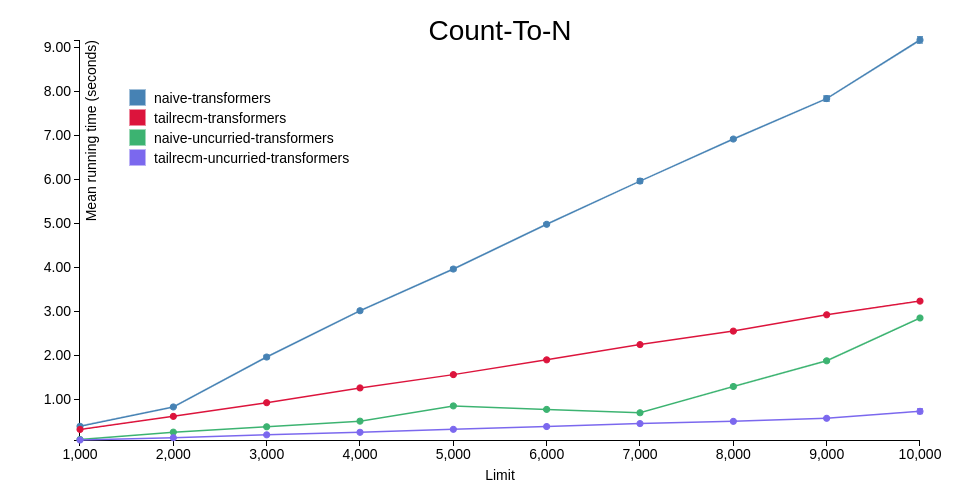
See the benchmark code here. For transformers, the RWST type with a Trampoline base is used, while for uncurried-transformers, the equivalent RWSET type is used with Identity as its base. In the following graphs, naive- means recursion is performed naively i.e. without the help of tailRecM; its presence corresponds to the tailrecm prefix instead.